

I have been building and studying crystal radios for some time now and slowly begin to learn a few things about these marvelous sets. In this section I begin my exploration of coil, coil quality and that mysterious dimensionless factor, Q... I start by presenting data on coil Q turfed up from web, with many thanks to those who publish their data! Secondly I present my own Q measurements on four "typical" coils I have laying about. Lastly I play with some Litz wire resistance calculations, just for the pleasure.

My purpose here is to present some facts and data that resulted from my explorations of the web. I have often wondered at what the quality factor of my coils should be and as often realized that I really do not have any expectations as to what is possible. Now, having done some research, I can with some confidence say that this is solved. Coils as used in crystal radio broadcast band reception typically employ coils with Q factors ranging from 100+ (pretty lousy) through the several 100's (decent) and on up to 1000 or more for those remarkable Big-Litz wonders ($$$). Knowing the expected (or actual) Q of your coil is important in so far as it impacts the choice of diode to be used in the set. On my page of Diode Calibration I present a summary graphic which indicates how the diode Rd value relates to the tank parallel resistance Rp. This Rp in turn is a function of the coil Q. Schezzam! So here we are.
In your set construction, with a good effort and good engineering practice one can easily expect to wind a solenoid coil in the Q = 200 range without much trouble, even with a cardboard form, sealed, of course. With various "open" coils, spiderweb, basket weave, diamond weave, etc. you may expect to double that.. possibly. The advantage in open coils derives from first the separation between adjacent wire turns which reduces self-capacitance in the coil, and secondly from the obvious lack of a form. All materials used in the coil will have some amount of dielectric losses associated with them and the less material used the better. Air core coils are best in this respect. I am not here to speak about ferrite coils as I have no experience with them. Frankly, they seem (to me) a bit like cheating.
The following graph presents data that I have scoured off the web. My primary sources include Hund and Groot, 1925*, Wes Hayward, Dave Schmarder, Ken Khun, Mike Tuggle, Steve Ratzlaff, and Dick Kleijer. 10,000 thanks for those who post their data on the web! This plot gives the Q value as a function of coil Rp (parallel resistance). In striving for a high Q coil, in effect one is eliminating losses and increasing parallel resistance (lowering series resistance) as much as possible. There is more to it of course. The Q formulas Qu = Rp / 2pifL and Qu = 2pifL / Rs tells us that Q is a function of the coil inductance L and the frequency f of the measurement as well as resistance.
All measurements chosen for plotting are made around 1 Mhz and most of the coils are in the L = 200 - 350 uH range. So, despite the formulas, in this plot the coil Rp is the main driver. From either plot it should be apparent that winding a coil with Q = 200 or better should be a no-brainer. If your coil Q is less, you just aren't trying. Most coils I have found to be in the Qu = 150 - 500 range. At the high end, Q's > 1000 seem to be pretty extreme and these coils are expensive. You better be using big Litz 660/46 and use a basket design (although the two best coils on the plot were solenoids, go figure!).
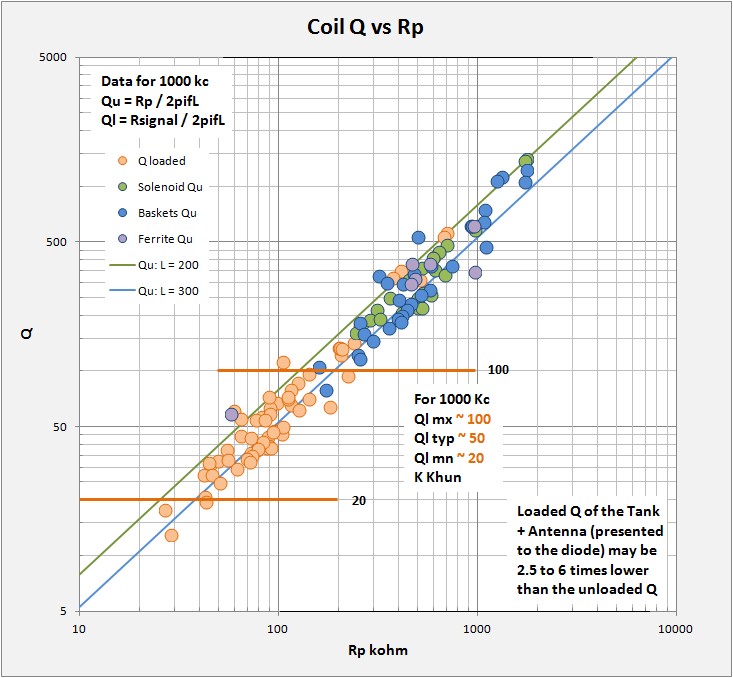
For this plot, green, blue, and purple circles are for published unloaded coil Q. I also post in orange circles an estimate of what the loaded Q presented to the diode (Antenna + Tank) might look like. Loaded Q will always be lower than the unloaded Q by several times. I have estimated that high-end sets (big litz, silver-plated ceramic insulated caps, best wiring practices) may lower the Q by about 2 1/2 times (B Tongue's performance set has Q = 700). At the low end (vintage components, small solid wire coils, taps) the load may lower Q by up to 6 times. Ken Khun in his excellent web book states that typical sets at 1Mhz have a loaded Q between 20 and 100, 50 typical and this is where most of my own data falls with the assumptions previously stated. I scaled the divisor by Qu to produce the above plot but note that this is merely an estimate. Having an idea of your set's Ql will allow a better selection of the proper diode for matching.

All the previous data was from published sources and all are for coil Q measurements made at or near 1MHz. It is interesting to look at how Q varies across the tuning range of the coil as well. Having had a chance to make a few Q measurements myself recently (Q2 2016) I finally have results to show and discuss, results across the broadcast band. The following data and plots result from the technique presented in the section "Coil Q Revisited". Calibrations for my measurements are based on capacitor Q measurements made on my behalf by Steve Ratzlaff AA7U with his HP Q-meter. It is worth to note that my capacitor used in these measurements has a low end capacitance of 8 pF, 18 pF and radio frequency. This allows measurements out to nearly 2.3 MHz.
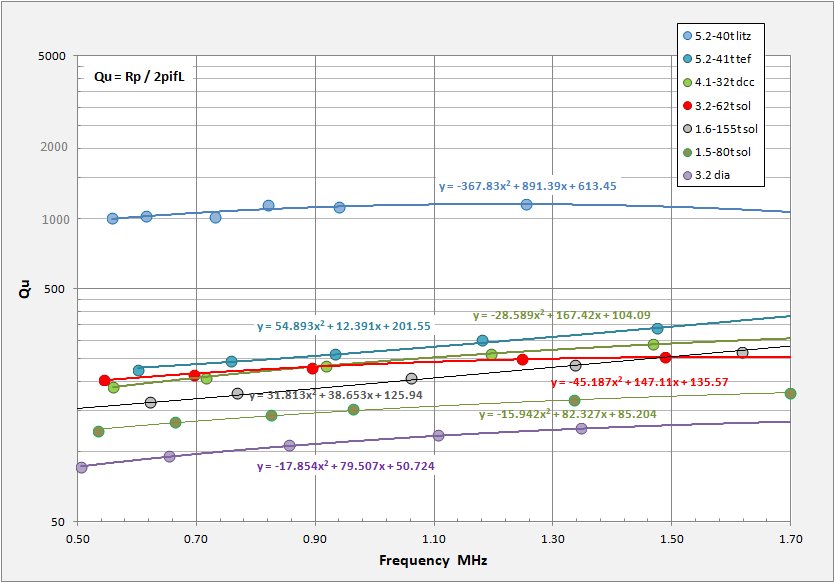
The above plot gives unloaded coil Q versus frequency for a set of several crystal set coils I have wound (or purchased in
the case of the diamond weave). I have chosen coils with what I had hoped to have a variety of performances, from a big
litz rope basket coil to a close wound tapped solenoid on cardboard stock from. I even threw in a couple small-gauge tp-form coils just to see how bad things can get (to offset the Litz as it were). The set includes the following coil
specs (note, coil photos at end of this section):
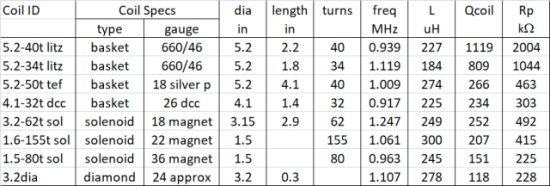
On the plot itself I post the measured data points and add a best-fit regression and formula describing the relation for each coil. Note that in most cases the regressions have fits with 0.99 or above except the litz coil with 0.88 and the 3.2" tapped solenoid with 0.98. Additionally I have added in grey a few lines of equal parallel resistance (for L=220 uH). These allow a visualization of how the coil Q relates to Rp according to the function Qu = Rp / 2pifL.
The graph clearly shows the litz coil with superior performance, the solenoid and DCC basket coils have similar moderate-low performance and the poor diamond-weave coil lies at the bottom. For the litz coil (light blue dots) and solenoid coil (red dots) we see a good curve with Q peaking in the middle of the band. With the silver-plated teflon insulated coil I originally had very high hopes. This wire does perform above average, but for its high price one would do well just to use big Litz. The diamond weave coil (purple dots) appears to be peaking near the top of the band. The curve for the DCC basket is interesting in that its Q peaks near the top of the band. The wire for this coil I bought on ebay and was disappointed when it arrived. While it has an absolutely beautiful green covering, the wire itself is small gauge, about 26awg and worse appeared to be plated. At first I assumed the plating was tin to protect the wire from corrosion. Because of skin effect the current in the wire concentrated on the outer wire surface at radio frequency. Therefore a plating can increase the resistance and losses. I find from my measurements that this wire in fact performs quite well and am currently assuming the plating is silver.
The general vision of a BCB coil with unloaded Q peaking in the middle of the band is instructive. Again I remind that the published data I have presented in the first part above is for 1MHz, near the "typical" peak Q. The coil Q's will certainly drop in the lower frequencies and possibly in the high as well.
Now a look at the coil Rp
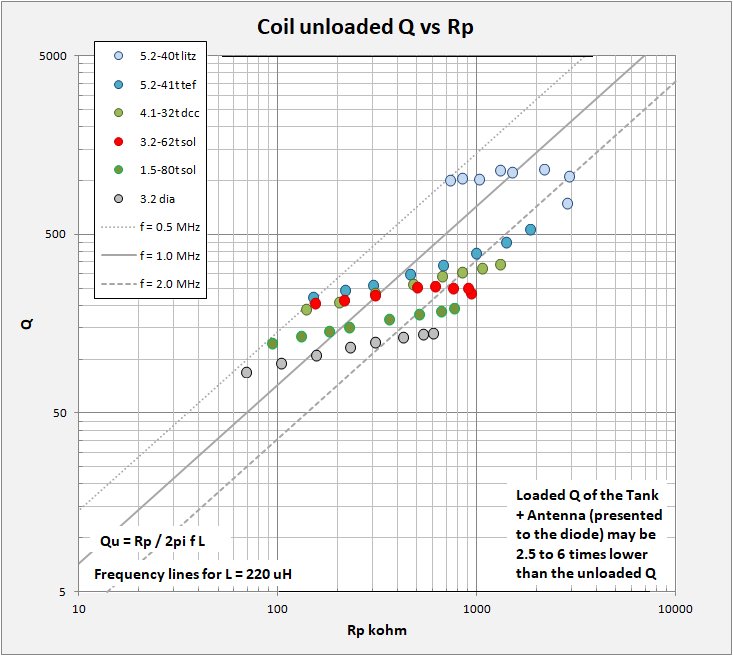
For a look at Rp I turn again to my favorite Q versus Rp plot. Tank Rp is the essential parameter one wishes to know for the purpose of matching tank to diode and load. Plot display and colors are as before and I have included some lines of constant frequency for the case of L = 220 uH, a pretty normal coil. This plot illustrates that, for any single coil, Rp is not constant across the entire broadcast band although at higher frequencies (above 2 MHz) some coils have a tendancy towards constant Rp. No single diode will be matched across the band for a single coil and Rp differences between different coils can be dramatic. Diode matching MUST be coil-specific. It seems good practice to choose your diode for a partictular coil at about f = 1MHz. Note that in this plot I give unloaded coil Q. When you load the coil with the capacitor, diode, antenna, and audio the Q (and therefore Rp) will drop somewhere between 2.5 to 6 times. I have attempted to illustrate this in my first "Coil Q vs Rp" plot at the beginning of the page.
Images of the tested coils, same scale.








A Calculation of 660-46 wire resistance in a high-end coil:
As much of the resistive loss is in the coil, keeping this to a minimum is important. The following discussion provides
a few calculations on Litz wire AC resistance. NOTE: THE ULTIMATE LIMIT ON COIL Q IS THE NEED TO USE WIRE!
From different Litz wire manufacturing sites one can find tables and data allowing the calculation of the resistance of
your favorite litz wire.
The formula for the D.C. resistance of any Litz construction is:
Rdc = Rs (1.0515)^Nb * (1.025)^Nc / Ns
Where:
Rdc = Resistance in Ohms/1000 ft.
Rs = Maximum D.C. resistance of the individual strands (4544 for 46awg wire)
Nb = Number of Bunching operations (assume = 2)
Nc = Number of Cabling operations (assume = 1)
Ns = Number of individual strands (assume = 660)
Rdc = 4544 (1.015)^2 (1.025)^1 / 660 = 7.27 ohms / 1000 ft.
The ratio of AC resistance to DC resistance of any Litz construction is:
Rac/Rdc = S + K (N Di / Do)^2 * G
Where:
S = Resistance ratio of individual strands when isolated (1.0003 for 46awg wire)
G = Eddy Current basis factor = (Di * sqrt(f) / 10.44)^4
F = Operating Frequency in HZ (assume 1MHz)
N = Number of strands in the cable = 660
Di = Diameter of the individual strands over the copper in inches = 0.0016
Do = Diameter of the finished cable over the strands in inches = 0.056
K = Constant depending on the number of strands = 2
Rac/Rdc = 1.0003 +2(660*0.0016 / 0.056)^2 * (0.0016*1000 / 10.44)^4 = 1.393
Therefore the AC Resistance of 660/46 litz wire is approximately :
The A.C. resistance is: 1.39 * 7.27 = 10.13 ohms/1000ft.
An example in real life:
For 53ft of Litz wire to wind a coil:
Rac = 53 * 10.13 ohm/1000ft
Rac = 0.54 ohms
For Qu = 2pifL / Rs
at 1 MHz and L = 230 uH
Qu = 2pi * 1 * 230 / 0.54ohms
Qu = 2692
A 5inch diameter basket weave coil made from 660/46 Litz wire having an inductance of 230 uH will typically require some 40 turns or about 53ft of wire. At 10.13 Ohm/kft, that comes to an AC wire resistance of 0.53 ohms for the coil alone. Were all the losses represented by series resistance of the wire, the coil would have, at 1 MHz an unloaded Q = 2700! This is as good as things can get. Naturally, wire resistance is not the only source of loss in the tank. There is a capacitor, metallic objects intruding into the magnetic field of the coil, dielectric losses, eddy current and other losses. Its no wonder that the best coils just top out just above Q = 1000 or so.
Time to get measuring. Below I provide my input data, have at it!
Kevin Smith
03/2013

*Note that in 1925 the importance of coil Rs was understood, but the factor Q was apparently not used. I have taken
(quite painfully) the L and Rs data from the Hund and Groot plots and calculated the resulting Q. I recommend to those interested to download the pdf of their paper.
https://archive.org/details/radiofrequency1925298hund
Modeled Data:
Radio-Frequency Resistance and Inductance of Coils used in Broadcast Reception: Series: Qu = 2pifL / Rs Parallel: Qu = Rp / 2pifL 1000 Khz Coil Type Wire Core Dia Length turns Rs Rp L Q Source awg type in in ohm Mohm uH solenoid 660/46 litz styrene 36 0.90 1.76 200 1400 Ratzlaff solenoid 660/46 litz styrene 4.50 3.00 44 0.91 1.73 200 1375 Hayward solenoid 175/46 litz air 5.00 2.88 0.96 265 579 Hayward solenoid 12 vinal plastic? 7.15 2.98 0.70 230 485 Kuhn solenoid 14 vinal plastic? 6.25 3.28 0.64 230 440 Kuhn solenoid 16 mgnt plastic? 3.45 3.18 57 3.52 0.59 230 410 Kuhn solenoid 18 mgnt plastic? 2.90 2.90 71 4.01 0.52 230 360 Kuhn solenoid 50/46 litz space wound 4.20 2.90 4.89 0.61 275 353 Hayward solenoid 32/38 litz hard rubber 3.31 2.41 65 6.20 0.68 327 331 Hund solenoid 20 mgnt plastic? 2.50 2.50 77 4.66 0.45 230 310 Kuhn solenoid 16 dcc hard rubber 6.65 2.73 40 7.60 0.53 319 264 Hund solenoid 28 dcc Varnish A 3.31 1.29 55 8.80 0.58 360 257 Hund solenoid 22 mgnt plastic? 2.10 2.76 88 5.78 0.36 230 250 Kuhn solenoid 24 dcc hard rubber 3.35 1.84 60 8.10 0.50 319 247 Hund solenoid 28 dcc Schellac 3.31 1.29 55 10.10 0.51 360 224 Hund solenoid 28 dcc Paraffin 3.31 1.29 55 10.30 0.50 360 220 Hund solenoid 50/46 litz close wound 4.20 1.52 53.25 10.84 0.52 378 219 Hayward solenoid 24 mgnt plastic? 1.80 2.29 94 6.72 0.31 230 215 Kuhn solenoid 28 dcc Varnish B 3.31 1.29 55 9.60 0.44 327 214 Hund solenoid 28 dcc hard rubber 3.31 1.29 55 9.70 0.41 319 207 Hund solenoid 26 mgnt plastic? 1.55 2.00 102 8.03 0.26 230 180 Kuhn solenoid 18 magnet cardboard 3.5 2.90 7.94 0.29 240 189 smith solenoid 22 magnet cardboard 1.5 4.30 8.67 0.32 265 192 smith solenoid 30 magnet cardboard 1.5 0.96 9.44 0.24 242 161 smith solenoid 28 dcc Spar Varnish 3.31 1.29 55 327 Hund basket weave 660/46 litz air 5.00 1.94 51 1.03 1.33 186 1134 Tuggle basket weave 660/46 litz air 5.00 2.25 42 1.08 1.26 186 1082 Tuggle basket weave 660/46 litz air 5.2 2.0 40 0.96 1.46 227 1591 smith basket weave 660/46 litz air 5.2 2.5 46 1.39 1.58 273 1169 smith spider 660/46 litz styrene 2.36 41 816 Kleijer Spider 165/46 hd polyethylene 1.75 4.75 55 1.94 1.09 232 750 Schmarder basket weave 175/46 litz air 5.00 36 2.56 1.08 265 650 Hayward spider 660/46 litz styrene 2.36 41 641 Kleijer Spider 100/45 hd polyethylene 1.75 4.25 55 2.41 0.93 238 620 Schmarder Spider 100/45 hd polyethylene 2.25 4.75 49 2.44 0.94 241 620 Schmarder Spider 100/45 hd polyethylene 2.25 4.75 39 1.73 0.51 149 540 Schmarder spider 175/46 polycarbonate 4.40 6.10 39 4.94 1.11 373 474 Hayward Loose Basket 32/38 litz air 3.78 5.30 0.75 317 376 Hund Spider 40/44 hd polyethylene 1.75 3.5 58 4.16 0.58 248 375 Schmarder Spider 40/44 hd polyethylene 1.75 3.5 56 4.16 0.48 225 340 Schmarder Spider 40/44 hd polyethylene 2.25 3.5 40 2.93 0.32 154 330 Schmarder basket 1 40/32 air 3.94 32 320 Kleijer basket 18 silver plate 5.4 4.2 40 3.90 0.35 187 301 smith basket 18 silver plate 5.4 4.2 46 4.74 0.42 225 298 smith Radial basket weave 32/38 hard rubber 2.61 7.50 0.58 331 277 Hund Loose Basket 24 dcc air 3.78 7.60 0.52 317 262 Hund basket weave 22 mgnt air 5.00 36 6.82 0.41 265 244 Hayward Loose Basket 28 dcc air 3.78 8.50 0.47 317 234 Hund Radial basket weave 24dcc hard rubber 2.61 9.50 0.44 327 216 Hund Narrow basket weave 32/38 air 3.10 10.40 0.42 332 201 Hund Radial basket weave 28dcc hard rubber 2.61 10.60 0.40 327 194 Hund Honeycomb 32/38 litz air 2.24 12.00 0.41 355 186 Hund basket 26 dcc 4 1.4 32 7.61 0.26 223 184 smith Radial basket weave 28dcc cardboard 2.65 12.00 0.36 330 173 Hund diamond 24 magnet air 3.2 0.3 10.49 0.27 267 160 smith Narrow basket weave 24 dcc air 3.10 13.80 0.30 323 147 Hund Narrow basket weave 28 dcc air 3.10 16.40 0.25 323 124 Hund Honeycomb 24 dcc air 2.24 18.50 0.26 347 118 Hund air torroid 24 dcc 5 14.34 0.16 242 106 smith Honeycomb 28 dcc air 2.33 27.50 0.17 347 79 Hund Spider 660/46 hd polyethylene 1.88 7 48 1.38 241 Schmarder Spider 660/46 hd polyethylene 1.88 6 39 0.90 150 Schmarder ferrite rod 50/46 litz ferrite juncbox 0.48 62 2.58 0.96 250 610 Hayward toroid 22 mgnt FT-114A-61 41 3.93 0.58 240 384 Hayward toroid 18 mgnt FT-114A-61 38 3.20 0.47 195 383 Hayward toroid 22 mgnt FT-114A-61 56 8.20 0.97 449 344 Hayward toroid 175/46 litz FT-114A-61 39 4.82 0.49 244 318 Hayward toroid 50/46 litz FT-114A-61 50 5.23 0.46 248 298 Hayward ferrite rod 22 mgnt R33-050-750 0.50 3.00 36 16.94 0.06 158 58.6 Hayward ferrite rod 22 mgnt ferrite juncbox 0.48 2.80 37 80 Hayward 2Layer Bank 32/38 litz Collodion 3.31 1.02 9.40 0.45 327 219 Hund 3Layer Bank 32/38 litz hard rubber 3.31 0.69 13.00 0.34 336 162 Hund 2Layer Bank 24 dcc Collodion 3.31 0.82 14.20 0.29 323 143 Hund 2Layer Bank 28 dcc hard rubber 3.31 16.80 0.25 323 121 Hund 4Layer Bank 32/38 litz hard rubber 3.31 0.49 19.50 0.26 360 116 Hund 3Layer Bank 24 dcc hard rubber 3.31 0.57 21.00 0.21 333 100 Hund 3Layer Bank 28 dcc hard rubber 3.31 0.41 24.00 0.18 333 87 Hund 4Layer Bank 24 dcc hard rubber 3.31 0.45 29.00 0.15 336 73 Hund 4Layer Bank 28 dcc hard rubber 3.31 0.29 32.50 0.14 336 65 Hund Double Layer 28 dcc hard rubber 3.31 inf 355 0 Hund

Data for measurements used in the plots for my own coils above:
f L C Q tank Q cap Qcoil Rp Rs D ESR MHz uH pF cal Mohm ohm ohm 5.2-34t litz Q of 34t Litz Basket 5.2 x 1.8 34t 2.136 202 28 58 283 72 196 37.35 0.013794 5.09 1.729 196 43 235 465 474 1007 4.49 0.002111 0.99 1.320 188 77 410 876 770 1201 2.03 0.001299 0.83 1.119 184 110 498 1294 809 1044 1.60 0.001237 0.96 0.893 178 179 612 2196 848 846 1.18 0.001179 1.18 0.707 172 295 664 3802 805 614 0.95 0.001242 1.63 0.620 169 391 721 5180 837 550 0.78 0.001195 1.82 5.2-40t litz Q of 40t Litz Basket 5.2 x 2.0 40t 2.266 266 19 172 182 744 2814 1.710 253 34 273 343 1062 2881 1.254 239 67 431 688 1152 2168 1.63 0.000868 0.46 0.939 227 127 605 1319 1119 1498 1.20 0.000894 0.67 0.819 222 170 698 1790 1144 1305 1.00 0.000874 0.77 0.730 217 219 707 2319 1017 1013 0.98 0.000983 0.99 0.614 210 319 790 3427 1027 833 0.79 0.000974 1.20 0.558 207 394 813 4253 1004 728 0.72 0.000996 1.37 5.2-46t litz Q of 46t Litz Basket 5.2 x 2.5 46t 2.149 308 18 174 174 1.888 301 24 214 232 1.494 289 39 296 393 1200 3260 2.26 0.000833 0.31 1.079 273 80 465 817 1081 2004 1.71 0.000925 0.50 0.881 264 124 572 1286 1031 1507 1.42 0.000970 0.66 0.738 256 182 631 1915 942 1118 1.26 0.001062 0.89 0.585 246 302 671 3230 847 765 1.07 0.001180 1.31 0.517 241 394 682 4253 813 635 0.96 0.001231 1.57 5.2-50t tef Q of 5.2" teflon solenoid, 274uH 5.2 x 4.3 50t 2.033 325 19 136 185 516 2139 8.03 0.001937 0.47 1.796 315 25 160 246 452 1608 7.86 0.002211 0.62 1.452 299 40 187 403 351 957 7.79 0.002853 1.04 1.239 288 57 203 581 312 700 7.19 0.003205 1.43 1.009 274 91 207 936 266 463 6.53 0.003755 2.16 0.812 260 148 219 1546 255 339 5.21 0.003920 2.95 0.659 248 235 211 2500 230 236 4.46 0.004347 4.24 0.522 234 396 204 4283 214 165 3.59 0.004664 6.07 5.2-41t tef Q of 5.2" teflon solenoid, 195uH 5.2 x 3.8 41t 2.320 237 20 143 195 533 1842 6.48 0.001875 0.54 2.080 231 25 162 250 457 1380 6.62 0.002190 0.72 1.779 223 36 187 358 393 982 6.35 0.002544 1.02 1.474 214 54 209 551 337 670 5.89 0.002964 1.49 1.179 204 89 227 920 301 455 5.02 0.003320 2.20 0.932 194 150 225 1576 262 298 4.32 0.003811 3.36 0.757 185 239 223 2541 244 215 3.60 0.004097 4.66 0.602 176 398 213 4300 224 149 2.97 0.004471 6.73 3.2-62t sol Q of 3.15" tapped solenoid, 233uH 3.2 x 3.1 62t 2.278 275 18 100 173 234 922 16.84 0.004274 1.08 2.090 272 21 114 210 250 892 14.25 0.003995 1.12 1.791 265 30 136 297 251 746 11.88 0.003991 1.34 1.488 257 45 162 449 254 610 9.43 0.003932 1.64 1.247 249 65 183 667 252 492 7.75 0.003972 2.03 0.893 236 135 197 1406 229 303 5.77 0.004362 3.30 0.695 226 232 197 2463 214 211 4.62 0.004676 4.73 0.544 217 393 195 4251 204 152 3.64 0.004895 6.59 2.7-65t sol Q of 2.7" Solenoid Coil, 236uH 2.7 x 2.4 65t 1.566 251 41 147 392 235 582 10.52 0.004251 1.72 1.381 247 54 166 588 231 494 9.28 0.004336 2.02 1.200 242 73 171 675 229 417 7.97 0.004374 2.40 1.014 236 105 179 866 226 339 6.64 0.004425 2.95 0.933 233 125 190 1322 222 303 6.15 0.004508 3.30 0.839 229 157 181 928 225 271 5.37 0.004449 3.68 0.717 224 220 176 1016 213 214 4.75 0.004705 4.66 0.496 212 485 164 3526 172 114 3.85 0.005825 8.81 4.1-32t dcc Q of 4.1" DCC Basket Coil, 230uH 4.1 x 1.4 32t 2.273 267 18 117 180 337 1286 11.30 0.002963 0.78 1.980 260 25 140 245 323 1046 10.01 0.003094 0.96 1.707 253 34 161 343 305 827 8.90 0.003281 1.21 1.467 246 48 181 484 289 656 7.82 0.003454 1.53 1.195 236 75 196 769 264 468 6.72 0.003790 2.14 0.917 225 134 201 1400 234 303 5.52 0.004266 3.30 0.716 214 231 191 2451 208 200 4.64 0.004818 5.00 0.560 204 395 181 4269 189 136 3.80 0.005278 7.34 3.2 dia Q of 3"Diamondweave Coil, 267uH 3.2 x 0.3 2.222 304 17 76 165 140 594 30.41 0.007158 1.68 2.031 301 20 82 201 139 533 27.63 0.007203 1.88 1.705 294 30 92 295 133 418 23.73 0.007536 2.39 1.347 285 49 100 495 125 302 19.23 0.007975 3.31 1.107 278 74 102 761 118 228 16.42 0.008496 4.39 0.856 269 129 99 1342 106 154 13.58 0.009402 6.51 0.654 259 228 92 2421 96 102 11.16 0.010467 9.81 0.507 251 393 84 4246 85 68 9.35 0.011702 14.64 1.6-155t sol Q of 1.55" tapped solenoid, 300uH 1.6 x 4.3 155t 2.081 329 18 116 174 351 1506 12.25 0.002851 0.66 1.885 324 22 127 216 306 1175 12.55 0.003268 0.85 1.617 318 30 142 303 266 857 12.16 0.003766 1.17 1.335 310 46 156 462 235 611 11.05 0.004251 1.64 1.061 300 75 163 768 207 415 9.65 0.004822 2.41 0.768 288 149 160 1565 178 248 7.78 0.005604 4.04 0.621 280 234 152 2491 162 177 6.74 0.006168 5.65 0.487 271 393 143 4251 148 123 5.60 0.006751 8.13 1.5-80t sol Q of 1in-80t, 267uH 1.5 x 1.0 80t 2.256 279 18 91 175 191 756 20.66 0.005229 1.32 2.036 275 22 101 219 186 652 18.92 0.005385 1.53 1.699 267 33 115 328 177 506 16.08 0.005638 1.98 1.335 258 55 128 559 167 360 12.98 0.006004 2.78 0.963 245 111 134 1155 151 225 9.80 0.006601 4.45 0.826 240 155 132 1624 143 178 8.69 0.006986 5.61 0.663 232 248 127 2641 134 129 7.23 0.007472 7.73 0.535 225 394 119 4256 122 92 6.17 0.008167 10.81
